TABE Math Test Prep
If you are serious about getting a great score on your TABE Math test, try out our recommended TABE Math Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A city stores its road salt in a large conical structure with a volume of 1206 cubic meters. The base of the container has a diameter of 24 meters. What is the height of the structure?
8 meters | |
6 meters | |
7 meters | |
5 meters |
Question 1 Explanation:
The correct answer is (A). The formula for the volume of a cone is on the TABE formula sheet. It is probably simplest to plug in each of the answer choices for $h$ (height) and see which results in the correct volume of 1206 cubic meters.
$V = \dfrac{1}{3} \pi r^2 h$
We know that: $π≅3.14$
To find our volume, $V$, we will also need a radius, $r$, and a height, $h$.
We are given that the diameter of the base is 24 meters. This means that the radius, which is half of the diameter, will be 12 meters.
We are trying to determine h by plugging in each answer choice. Beginning with $h$ = 8 we have:
$V = \dfrac{1}{3} \pi r^2 h$
$V=\dfrac{1}{3} (3.14) (12)^2 (8) $ $ = 1205.76$
It turns out that this is the value closest to the given volume of 1206 cubic meters.
So, $h$ = 8 meters is the correct choice.
$V = \dfrac{1}{3} \pi r^2 h$
We know that: $π≅3.14$
To find our volume, $V$, we will also need a radius, $r$, and a height, $h$.
We are given that the diameter of the base is 24 meters. This means that the radius, which is half of the diameter, will be 12 meters.
We are trying to determine h by plugging in each answer choice. Beginning with $h$ = 8 we have:
$V = \dfrac{1}{3} \pi r^2 h$
$V=\dfrac{1}{3} (3.14) (12)^2 (8) $ $ = 1205.76$
It turns out that this is the value closest to the given volume of 1206 cubic meters.
So, $h$ = 8 meters is the correct choice.
Question 2 |
100 attendees of a professional rodeo were randomly selected, and two aspects of their attire were noted. The results are shown in the two-way frequency table below.
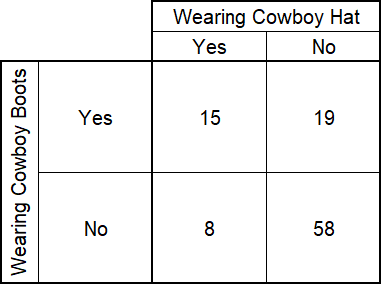
Given that a selected attendee is wearing a cowboy hat, what is the probability that the attendee is wearing cowboy boots? Round your answer to two decimal places.
0.65 | |
0.34 | |
0.23 | |
0.15 |
Question 2 Explanation:
The correct answer is (A). When you see the phrase “given that” in a probability question, it is highly likely that you are being asked to find a conditional probability.
This problem begins by stating “Given that a selected attendee is wearing a cowboy hat”. As soon as we see the term “given that”, we need to immediately focus in on what comes next — “wearing a cowboy hat” — and ignore anyone/anything that does not meet this condition:
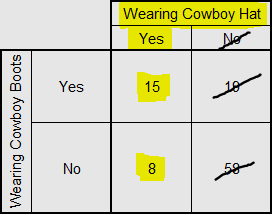
We are only focusing on the 23 (15 + 8) attendees that are wearing a cowboy hat — highlighted above in yellow — and ignore everyone not wearing a cowboy hat.
We can now move onto the second part of the question which states “…what is the probability that the attendee is wearing cowboy boots?”
Out of the 23 attendees wearing a cowboy hat, we can see that 15 are wearing cowboy boots:
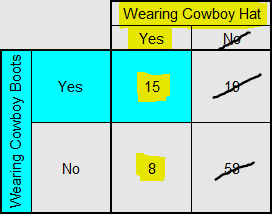
15 out of 23 can be expressed as the fraction $\frac{15}{23}$ or the decimal 0.652.
Rounding to two decimals, we have: 0.65
This problem begins by stating “Given that a selected attendee is wearing a cowboy hat”. As soon as we see the term “given that”, we need to immediately focus in on what comes next — “wearing a cowboy hat” — and ignore anyone/anything that does not meet this condition:

We are only focusing on the 23 (15 + 8) attendees that are wearing a cowboy hat — highlighted above in yellow — and ignore everyone not wearing a cowboy hat.
We can now move onto the second part of the question which states “…what is the probability that the attendee is wearing cowboy boots?”
Out of the 23 attendees wearing a cowboy hat, we can see that 15 are wearing cowboy boots:

15 out of 23 can be expressed as the fraction $\frac{15}{23}$ or the decimal 0.652.
Rounding to two decimals, we have: 0.65
Question 3 |
A certain car sold in Australia has its fuel efficiency stated as 5.4 liters per 100 kilometers. In other words, with 5.4 liters of gasoline, the car can travel 100 kilometres.
If this same car were sold in the USA, its fuel efficiency would need to be provided in miles per gallon (MPG). What would be the correct MPG for this car?
Remember that the TABE Formula Sheet provides unit conversion information.
51 miles per gallon | |
46 miles per gallon | |
44 miles per gallon | |
49 miles per gallon |
Question 3 Explanation:
The correct answer is (C). The unit conversions are on the TABE formula sheet. To end up with miles per gallon, we will want to begin with the units of distance on top (in the numerator) and the units of volume on the bottom (in the denominator):
$\dfrac{100 \text{ km}}{5.4 \text{ l}}$
Next, we will convert the kilometers to miles and the liters to gallons:
$\require{cancel} \dfrac{100 \cancel{\text{km}}}{5.4 \cancel{\text{l}}} \cdot \dfrac{3.8 \cancel{\text{l}}}{1 \text{ gal}} \cdot \dfrac{0.62\text{ mi}}{1 \cancel{\text{km}}}$
$\dfrac{(100)(3.8)(0.62 \text{ mi})}{(5.4)(1 \text{ gal})(1)} $ $ = \dfrac{235.6 \text{ mi}}{5.4 \text{ gal}}$
$43.6 \, \dfrac{\text{mi}}{\text{gal}} \approx 44 \, \dfrac{\text{mi}}{\text{gal}}$
$\dfrac{100 \text{ km}}{5.4 \text{ l}}$
Next, we will convert the kilometers to miles and the liters to gallons:
$\require{cancel} \dfrac{100 \cancel{\text{km}}}{5.4 \cancel{\text{l}}} \cdot \dfrac{3.8 \cancel{\text{l}}}{1 \text{ gal}} \cdot \dfrac{0.62\text{ mi}}{1 \cancel{\text{km}}}$
$\dfrac{(100)(3.8)(0.62 \text{ mi})}{(5.4)(1 \text{ gal})(1)} $ $ = \dfrac{235.6 \text{ mi}}{5.4 \text{ gal}}$
$43.6 \, \dfrac{\text{mi}}{\text{gal}} \approx 44 \, \dfrac{\text{mi}}{\text{gal}}$
Question 4 |
A portion of the graph of a linear equation with two variables, x and y, is shown below. Based on the graph, which of the following is not a solution to the equation?

(4, −5) | |
(−2, 7) | |
(−3, 9) | |
(6, −10) |
Question 4 Explanation:
The correct answer is (D). All combinations of x and y coordinates that lie on the graph are solutions to the equation that created the red graph.
The points (4, −5) and (−2, 7) clearly lie on the graph. When x = 4, y = −5 and when x = −2, y = 7.
The other two answer choices are not actually shown on the visible portion of the graph. However, we know that the graph is linear, which means that x and y change at a constant rate relative to one another. We can observe that each time x increases by 1, y decreases by 2, and when x decreases by 1, y increases by 2.
Since (−2, 7) is on the graph, the point (−3, 9) will also be on the graph. And, since (5, −7) is on the graph, the point (6, −9) will also be on the graph. Thus, the point (6, −10) does not lie on the graph and, therefore, is not a solution to the linear equation that created the graph.
The points (4, −5) and (−2, 7) clearly lie on the graph. When x = 4, y = −5 and when x = −2, y = 7.
The other two answer choices are not actually shown on the visible portion of the graph. However, we know that the graph is linear, which means that x and y change at a constant rate relative to one another. We can observe that each time x increases by 1, y decreases by 2, and when x decreases by 1, y increases by 2.
Since (−2, 7) is on the graph, the point (−3, 9) will also be on the graph. And, since (5, −7) is on the graph, the point (6, −9) will also be on the graph. Thus, the point (6, −10) does not lie on the graph and, therefore, is not a solution to the linear equation that created the graph.
Question 5 |
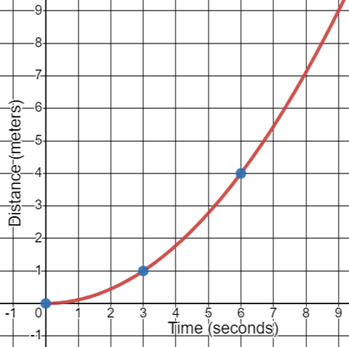
In graph below, the y-axis shows the distance an object has traveled (in meters) in the elapsed time (in seconds) shown on the x-axis. For example, the coordinate (3,1) means that after 3 seconds, the object has traveled 1 meter.
Using the information shown in the graph, at what average speed does the object travel in the elapsed time from 0 seconds to 6 seconds? Round to the nearest tenth.
1.5 m/s | |
1.1 m/s | |
0.7 m/s | |
0.4 m/s |
Question 5 Explanation:
The correct answer is (C). To find average speed, we need to divide the total distance travelled (the “change in distance”) by the total time elapsed (the “change in time”):
$\dfrac{(4 − 0) \text{ meters}}{(6 − 0) \text{ seconds}} = \dfrac{4 \text{ meters}}{6 \text{ seconds}}$
$= \dfrac{2 \text{ meters}}{3 \text{ seconds}} \cong 0.7 \, \dfrac{\text{m}}{\text{s}}$
$\dfrac{(4 − 0) \text{ meters}}{(6 − 0) \text{ seconds}} = \dfrac{4 \text{ meters}}{6 \text{ seconds}}$
$= \dfrac{2 \text{ meters}}{3 \text{ seconds}} \cong 0.7 \, \dfrac{\text{m}}{\text{s}}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
|
List |
