This is our second free TABE Math practice test. It covers Level M, which is considered to be medium difficulty. Some of the topics at this level include measurement, geometry, equations, fractions, ratios, and algebraic thinking. Continue your test prep now with our TABE Math Level M practice questions!
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
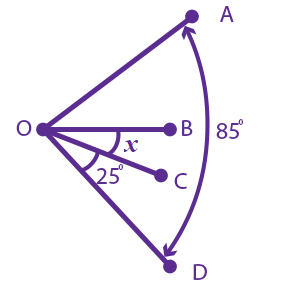
In the figure below (not drawn to scale), the measure of Angle COD is 25°. The measure of Angle AOB is twice the measure of Angle COD. The measure of Angle AOD is 85°. What is the value of x, the measure of Angle BOC?
5 | |
20 | |
15 | |
10 |
Question 1 Explanation:
The correct answer is (D). The measure of Angle COD is 25°. Since the measure of Angle AOB is twice the measure of Angle COD, it is 50°.
The measure of Angle AOD is 85° and is the sum of the measures of Angles AOB, COD, and BOC.
m∠AOD = m∠COD + m∠AOB + m∠BOC
85 = 25 + 50 + x
85 = 75 + x
x = 10
The measure of Angle AOD is 85° and is the sum of the measures of Angles AOB, COD, and BOC.
m∠AOD = m∠COD + m∠AOB + m∠BOC
85 = 25 + 50 + x
85 = 75 + x
x = 10
Question 2 |
What is the total distance, in meters, traveled by a slug that first travels 400 millimeters and then travels an additional 30 centimeters?
0.430 meters | |
0.340 meters | |
0.304 meters | |
0.700 meters |
Question 2 Explanation:
The correct answer is (D). Since we are computing the total distance in meters, it will be helpful to convert each measurement to meters.
To convert millimeters to meters, we divide by 1000, which means moving the decimal 3 places to the left. 400 millimeters is equivalent to 0.400 meters.
To convert centimeters to meters, we divide by 100, which means moving the decimal 2 places to the left. 30 centimeters is equivalent to 0.30 meters.
When we add 0.400 meters to 0.30 meters, we get 0.700 meters.
To convert millimeters to meters, we divide by 1000, which means moving the decimal 3 places to the left. 400 millimeters is equivalent to 0.400 meters.
To convert centimeters to meters, we divide by 100, which means moving the decimal 2 places to the left. 30 centimeters is equivalent to 0.30 meters.
When we add 0.400 meters to 0.30 meters, we get 0.700 meters.
Question 3 |
In the number 815.927, the digit “2” represents a value equivalent to which of the following?
$2×\left(\dfrac{1}{10}\right)$ | |
$2×(1)$ | |
$2×\left(\dfrac{1}{1000}\right)$ | |
$2×\left(\dfrac{1}{100}\right)$ |
Question 3 Explanation:
The correct answer is (D). The digit “2” is in the hundredths place, meaning that we have “two hundredths” which can be written as $2×\left(\frac{1}{100}\right)$.
Question 4 |
Jacob promises to give Miriam two-fifths of his part of the reward. His part of the reward is $\frac{3}{7}$. To figure out what fraction of the reward she will receive, she sets up the following:
$\dfrac{2}{5} \times \dfrac{3}{7} = \; ?$What fraction will she receive?
$\dfrac{6}{35}$ | |
$\dfrac{5}{12}$ | |
$\dfrac{15}{14}$ | |
$\dfrac{29}{35}$ |
Question 4 Explanation:
The correct answer is (A). When multiplying fractions, we simply multiply the numerators to find the numerator of the answer and multiply the denominators to find the denominator of the answer. Remember: there is no need for a common denominator when multiplying or dividing fractions.
$\dfrac{2}{5} \times \dfrac{3}{7} = \dfrac{2 \times 3}{5 \times 7} = \dfrac{6}{35}$
$\dfrac{2}{5} \times \dfrac{3}{7} = \dfrac{2 \times 3}{5 \times 7} = \dfrac{6}{35}$
Question 5 |
When dividing $\frac{1}{3}$ of a pizza into 4 equal slices what fraction of the original whole pizza will each slice be?
$\dfrac{1}{4}$ | |
$\dfrac{4}{3}$ | |
$\dfrac{1}{7}$ | |
$\dfrac{1}{12}$ |
Question 5 Explanation:
The correct answer is (D). Here we are dividing the fraction $\frac{1}{3}$ into 4 equal slices. This can be expressed mathematically as: $\frac{1}{3} ÷ 4$
Dividing by 4 is the same as multiplying by its reciprocal,$\frac{1}{4}$.
$\dfrac{1}{3} ÷ 4 = \dfrac{1}{3} \times \dfrac{1}{4} $ $ = \dfrac{1 \times 1}{3 \times 4} = \dfrac{1}{12}$
Each slice will be $\frac{1}{12}$ of the original whole pizza.
Dividing by 4 is the same as multiplying by its reciprocal,$\frac{1}{4}$.
$\dfrac{1}{3} ÷ 4 = \dfrac{1}{3} \times \dfrac{1}{4} $ $ = \dfrac{1 \times 1}{3 \times 4} = \dfrac{1}{12}$
Each slice will be $\frac{1}{12}$ of the original whole pizza.
Question 6 |
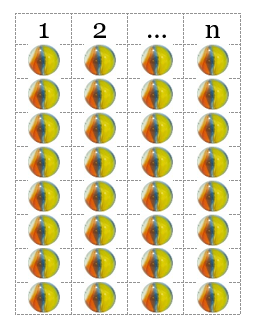
Each column, 1 through n, contains 8 marbles. If we want 72 total marbles, what will be the value of n ?
8 | |
6 | |
9 | |
7 |
Question 6 Explanation:
The correct answer is (C). Each column contains 8 marbles. We have $n$ columns of 8 marbles. What does $n$ need to be so that we have 72 marbles altogether?
Expressed algebraically we have: $8 × n = 72$
To make this a true statement: $n = 9$
Expressed algebraically we have: $8 × n = 72$
To make this a true statement: $n = 9$
Question 7 |
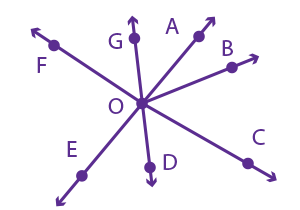
In the figure above $\overleftrightarrow{AE} \perp\overleftrightarrow{FC}$ (“line AE is perpendicular to line FC”).
Which two rays form an obtuse angle?
$\overrightarrow{\rm OF}\,$ and $\,\overrightarrow{\rm OG}$ | |
$\overrightarrow{\rm OA}\,$ and $\,\overrightarrow{\rm OD}$ | |
$\overrightarrow{\rm OE}\,$ and $\,\overrightarrow{\rm OC}$ | |
$\overrightarrow{\rm OB}\,$ and $\,\overrightarrow{\rm OC}$ |
Question 7 Explanation:
The correct answer is (B). We are told that $\overleftrightarrow{AE} \perp\overleftrightarrow{FC}$. This means the two lines form a right angle (90°). An obtuse angle is an angle that is greater than 90° (and less than 180°).
Only $\overrightarrow{\rm OA}$ and $\overrightarrow{\rm OD}$ form an angle greater than 90°. The rays of answer choices (A) and (D) create acute angles (less than 90°), and the rays of answer choice (C) create a right angle.
Only $\overrightarrow{\rm OA}$ and $\overrightarrow{\rm OD}$ form an angle greater than 90°. The rays of answer choices (A) and (D) create acute angles (less than 90°), and the rays of answer choice (C) create a right angle.
Question 8 |
Which of the following values for x is a solution to the equation below?
$x \cdot (x - 2) > 7$
$x = 2$ | |
$x = −1$ | |
$x = 3$ | |
$x = −2$ |
Question 8 Explanation:
The correct answer is (D). There is no need to use algebra here. Instead, try each of the answer choices to determine which one results in a true statement:
When $x=2$ we have:
$(2)(2-2)>7→ $ $(2)(0)>7→0>7$
This is false; 0 is not greater than 7.
When $x=-1$ we have:
$(-1)(-1-2)>7→ $ $ (-1)(-3)>7→3>7$
This is false; 3 is not greater than 7.
When $x=3$ we have:
$(3)(3-2)>7→ $ $ (3)(1)>7→3>7$
This is false; 3 is not greater than 7.
When $x=-2$ we have:
$(-2)(-2-2)>7→ $ $ (-2)(-4)>7→8>7$
This is true; 8 is greater than 7.
When $x=2$ we have:
$(2)(2-2)>7→ $ $(2)(0)>7→0>7$
This is false; 0 is not greater than 7.
When $x=-1$ we have:
$(-1)(-1-2)>7→ $ $ (-1)(-3)>7→3>7$
This is false; 3 is not greater than 7.
When $x=3$ we have:
$(3)(3-2)>7→ $ $ (3)(1)>7→3>7$
This is false; 3 is not greater than 7.
When $x=-2$ we have:
$(-2)(-2-2)>7→ $ $ (-2)(-4)>7→8>7$
This is true; 8 is greater than 7.
Question 9 |
If 1081 marbles are divided equally amongst 47 bowls, how many marbles will there be in each bowl?
21 | |
23 | |
31 | |
33 |
Question 9 Explanation:
The correct answer is (B). You can either use the standard long division algorithm (shown below) or you can work backwards from the answer choices (e.g. multiply each answer choice by 47 to see which answer results in 1081 marbles).

If you are struggling with long division, you can watch a Khan Academy video HERE.

If you are struggling with long division, you can watch a Khan Academy video HERE.
Question 10 |
A package that contains 10 kilograms (kg) of sugar has a selling price of \$4. How many kilograms of sugar can be purchased for \$1?
0.40 kg | |
0.25 kg | |
2.5 kg | |
4.0 kg |
Question 10 Explanation:
The correct answer is (C). 10 kg per \$4 can be expressed as the ratio 10:4 and the fraction $\frac{10}{4}$ .
$\frac{10}{4}$ can be reduced to $\frac{5}{2}$. This makes sense since if we can buy 10 kg for \$4, it makes sense that we could buy half the amount of sugar, 5 kg, for half the money, \$2.
$\frac{5}{2}$ is the same as 5 ÷ 2 = 2.5.
2.5 kg of sugar can be purchased for \$1.
$\frac{10}{4}$ can be reduced to $\frac{5}{2}$. This makes sense since if we can buy 10 kg for \$4, it makes sense that we could buy half the amount of sugar, 5 kg, for half the money, \$2.
$\frac{5}{2}$ is the same as 5 ÷ 2 = 2.5.
2.5 kg of sugar can be purchased for \$1.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
