TABE Math Test Prep
If you are serious about getting a great score on your TABE Math test, try out our recommended TABE Math Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If you first add 4 to Thomas’ age and then multiply this sum by 3, you will have his father’s age of 51 years old.
Which of the following properly represents this statement algebraically?
$4t + 3 = 51$ | |
$3t + 4 = 51$ | |
$4(t + 3) = 51$ | |
$3(t + 4) = 51$ |
Question 1 Explanation:
The correct answer is (D). Let t represent Thomas’ age, the unknown in this question.
We are told to “first add 4 to Thomas’ age”:
$t + 4$
We are next told to “multiply this sum by 3”:
$3(t + 4)$
Finally, we know that this result is equal to 51:
$3(t + 4) = 51$
We are told to “first add 4 to Thomas’ age”:
$t + 4$
We are next told to “multiply this sum by 3”:
$3(t + 4)$
Finally, we know that this result is equal to 51:
$3(t + 4) = 51$
Question 2 |
What sequence of transformations on the blue shape will result in the red shape?
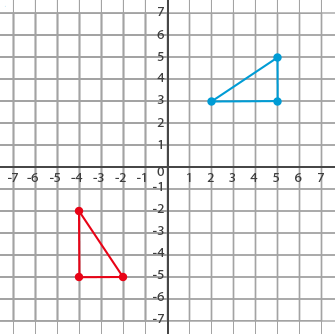
Reflect across the x-axis then reflect across the y-axis | |
Reflect across the y-axis then translate 8 units down | |
Translate 6 units to the left then translate 8 units down | |
Rotate 90° clockwise then translate 7 units to the left |
Question 2 Explanation:
Of the four answer choices given, only answer (D) will result in the red shape.
Answer (A) results in the following:
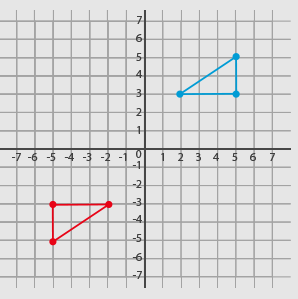
Answer (B) results in the following:
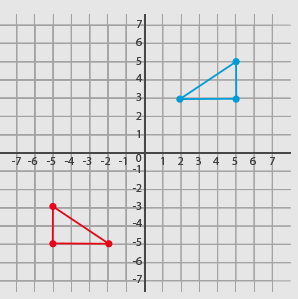
Answer (C) results in the following:
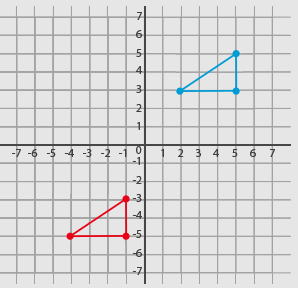
Answer (A) results in the following:

Answer (B) results in the following:

Answer (C) results in the following:

Question 3 |
In a large storage room comprised of vertical walls with a flat roof, the distance from A to B measures 40 feet. In the same storage room, the distance from A to C is found to be 41 feet.
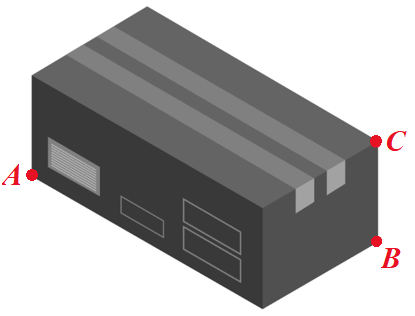
Using this information, what would be the expected height of the storage room?
7 feet | |
8 feet | |
9 feet | |
10 feet |
Question 3 Explanation:
The key is to recognize that connecting A, B, and C forms a right triangle with a leg (AB) of 40 feet and a hypotenuse (AC) of 41 feet.
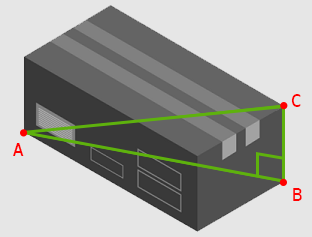
Using the Pythagorean Theorem, which is given on the TABE formula sheet, we can determine the height (BC):
$a^2 + b^2 = c^2$
$(AB)^2 + (BC)^2 = (AC)^2$
$40^2 + (BC)^2 = 41^2$
$1600 + (BC)^2 = 1681$
$(BC)^2 = 1681 - 1600$
$(BC)^2 = 81$
$BC = \sqrt{81}$
$BC = 9$ (only the positive square root makes sense)

Using the Pythagorean Theorem, which is given on the TABE formula sheet, we can determine the height (BC):
$a^2 + b^2 = c^2$
$(AB)^2 + (BC)^2 = (AC)^2$
$40^2 + (BC)^2 = 41^2$
$1600 + (BC)^2 = 1681$
$(BC)^2 = 1681 - 1600$
$(BC)^2 = 81$
$BC = \sqrt{81}$
$BC = 9$ (only the positive square root makes sense)
Question 4 |

How much money per pretzel do you save when you buy “3 pretzels for $10” as compared to the cost per pretzel when you only by “1 pretzel for $4”?
$1.00 | |
$0.67 | |
$0.33 | |
$0.40 |
Question 4 Explanation:
The correct answer is (B). We know that 1 pretzel costs \$4, therefore its unit price (price per pretzel) is \$4.00.
To figure out how much we save, we will need to first determine the unit price when buying “3 pretzels for \$10”. To do so, we need to divide \$10 by 3 pretzels:
$\$10 ÷ 3 = \$3.33$$\text{ per} \text{ pretzel}$
To determine the savings, we find the difference in the unit prices:
$\$4.00 − \$3.33 = \$0.67$
To figure out how much we save, we will need to first determine the unit price when buying “3 pretzels for \$10”. To do so, we need to divide \$10 by 3 pretzels:
$\$10 ÷ 3 = \$3.33$$\text{ per} \text{ pretzel}$
To determine the savings, we find the difference in the unit prices:
$\$4.00 − \$3.33 = \$0.67$
Question 5 |
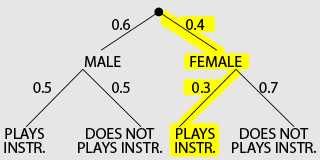
A survey of adult visitors of a famous rock and roll museum is conducted. The results of the survey are summarized in the following probability tree diagram.

Based on the tree diagram, what is the probability that an adult visitor to the museum is female and plays an instrument?
0.30 | |
0.36 | |
0.12 | |
0.70 |
Question 5 Explanation:
The correct answer is (C). A tree diagram is one way to present the probabilities of compound events.
In this example, the probability that an adult visitor to the museum is female is 0.4. The probability that an adult female visitor to the museum plays an instrument is 0.3.
To find the compound probability that “an adult visitor is female and plays an instrument” we must multiply our probabilities:
$0.4 × 0.3 = 0.12$
In this example, the probability that an adult visitor to the museum is female is 0.4. The probability that an adult female visitor to the museum plays an instrument is 0.3.
To find the compound probability that “an adult visitor is female and plays an instrument” we must multiply our probabilities:
$0.4 × 0.3 = 0.12$

Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
|
List |
